Sepsis-3
sep.RmdMedical Background
Sepsis is a life-threatening reaction to an infection that causes damage to different tissues and organs in the body. It remains a major public health issue associated with high mortality, morbidity, and related health costs [1–4]. The current clinical gold standard for identifying sepsis is the so-called Sepsis-3 consensus, which highlighted the central role of organ dysfunction in the definition, identification, prognostication, and pathophysiological understanding of sepsis [5].
After a sepsis onset, delay in effective antimicrobial therapy, significantly increases mortality [ferrer2014, pruinelli2018, seymour2017]. Furthermore, sepsis is a complex and heterogeneous syndrome, potentially reversible in its early stages, yet difficult to identify, while its more advanced stages become easier to recognize, but also more challenging to successfully treat [7]. Unfortunately, identifying bacterial species in blood samples can take up to 48 hours [8], causing significant and potentially detrimental delays in confirming a suspected infection. Meanwhile, an abundance of clinical and laboratory data is being routinely collected, the richest set of which is accumulated in the intensive care unit (ICU). While it has become harder for intensivists to manually process the increasing quantities of patient information [9], machine learning (ML) systems have the potential to leverage this data in order to provide alarm systems that can aid the clinician in recognizing sepsis in its early stages, which can possibly lead to earlier treatment and better patient outcomes in the ICU.
Suggested Prediction Problem
According to sepsis-3 consensus, sepsis is defined by the co-occurrence of the following two:
- suspected infection (defined as antibiotic treatment and body fluid sampling within a specified time window),
- an acute increase in the SOFA [10] score which measures the degree of organ dysfunction.
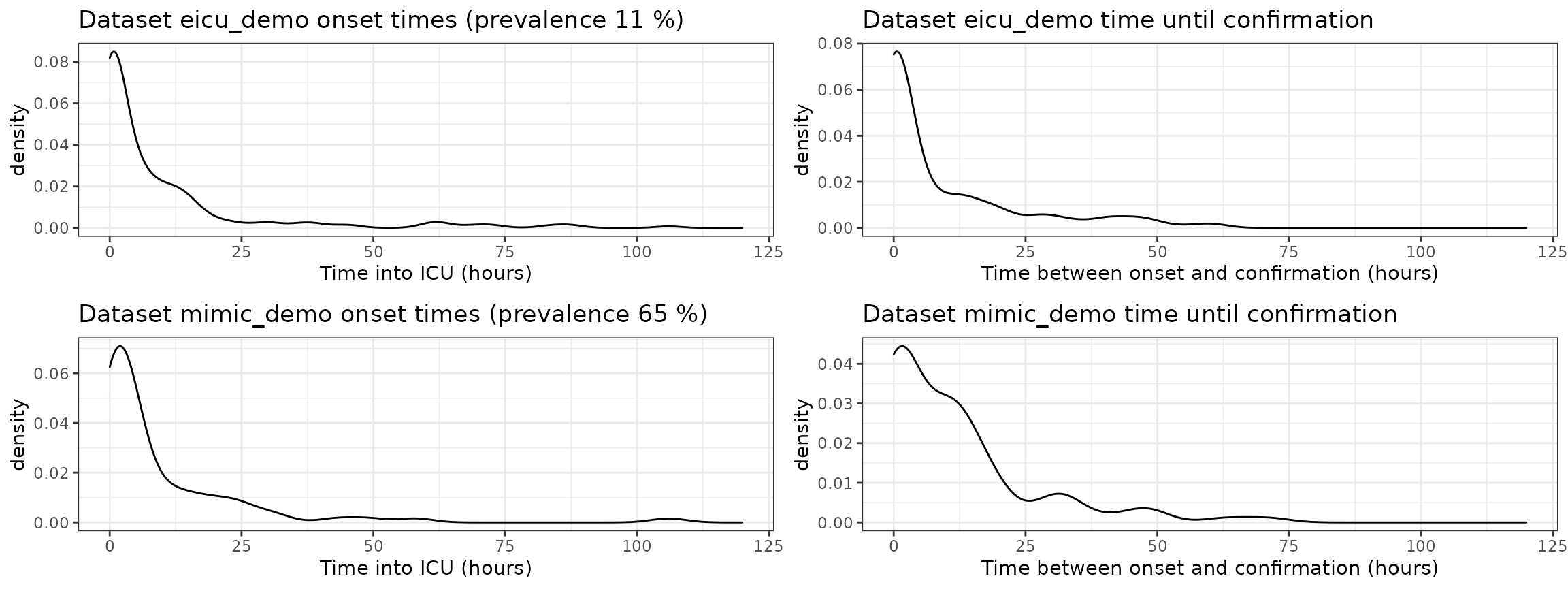
A graphical representation of how a sepsis-3 onset might occur in the ICU.
In particular, as the above figure indicates, suspected infection (SI, for short), is defined as:
- antibiotic administration (labeled ABX) at time \(t_{abx}\) followed by body fluid sampling (Sampling, at time \(t_{samp}\)) within a 24 hour window
- body fluid sampling followed by antibiotic administration within a 72 hour window
The earlier of the two times is taken as the time of suspected infection. Then, a 72 hour window is spanned around the SI time (48 hours prior, 24 hours after). Within this SI window, the level of the SOFA score is monitored, and an increase of 2 or more points defines the onset of sepsis, and this time is labeled \(t_{sep3}\) (the earliest such time is taken, if any exists, and subsequent increases are ignored).
Sepsis-3 is not a stopping time
The onset of sepsis-3 is not a stopping time [11]. That is, at time when the sepsis-3 onset occurs, it is not necessarily possible to verify that the onset occurred (for example, consider a SOFA increase of 2 points at 0 hours, followed by body fluid sampling at 24 hours, and antibiotic treatment at 48 hours; in this case, the sepsis-3 event occurring at 0 hours is only confirmed 48 hours later).
The following parameters are especially relevant for the prediction problem: \[\begin{align*} L &= \text{how early prior to onset is the prediction valid} \\ R &= \text{how much in advance is the prediction valid} \\ \end{align*}\]
We consider the choices of \(L = 24\) hours and \(R = t_{confirm} := \max\Big(t_{samp}, t_{abx}, t_{sep3}\Big)\) as appropriate. In words, an alarm is considered to be timely if it happens no earlier than 24 hours before the sepsis-3 onset. Furthermore, the alarm is considered to be informative if it happens no later than the time at which sepsis-3 can be definitively confirmed.
Finally, when designing an alarm system, to prevent alarm fatigue, alarms cannot ring too frequently, so we consider using alarm silencing, defined by the parameter:
\[\begin{align*} \delta = \text{duration of alarm silencing after the alarm is raised} \end{align*}\]
For sepsis-3, we consider the fixed value of \(\delta = \infty\) hours, meaning that the alarm system is silenced indefinitely after it is raised for the first time.
Dataset limitations
There are two major data limitations when trying to compute the sepsis-3 labels on the publicly available datasets considered in this repository. In particular, we highlight that:
- eICU dataset reports body fluid sampling information for only a very small fraction of patients,
- HiRID dataset reports no body fluid sampling information.
For this reason, an alternative definition needs to be used for these datasets. The alternative definition requires two or more antibiotic administrations within a 24-hour window.
Reproducible Code
After defining the prediction problem and the key parameters, we provide code that can be used to generate data which is ready for AI prediction models.
srcs <- c("mimic_demo", "eicu_demo")
phys <- c(
"alt", "alp", "ast", "basos", "bicar", "bili", "ca", "cai", "tco2", "cl",
"crea", "dbp", "eos", "fio2", "hr", "hct", "hgb", "inr_pt", "lact", "lymph",
"mg", "mch", "mchc", "mcv", "map", "neut", "o2sat", "pco2", "po2", "ph",
"phos", "plt", "k", "pt", "ptt", "rdw", "rbc", "resp", "na", "sbp", "bun",
"wbc", "temp", "alb", "ck", "etco2", "crp", "gcs", "pafi", "safi",
"map_beta50", "map_beta100", "map_beta200", "be", "bili_dir", "bnd", "ckmb",
"esr", "fgn", "glu", "bmi", "age"
)
meds <- c("cortico", "mech_vent", "dex_amount", "ins_ifx")
dat <- load_concepts(c(phys, meds), srcs, verbose = FALSE)
# carry-forward for physiological variable
dat <- fill_gaps(dat)
dat <- replace_na(dat, type = "locf", vars = phys)
# 0-imputation for treatment variables
dat <- replace_na(dat, 0, vars = meds)
# obtain onset information
sep3 <- sep3_info(srcs)
dat <- merge(dat, sep3, all.x = TRUE)
# remove times after t_confirm
dat <- dat[, t_confirm := max_or_na(t_confirm), by = c(id_vars(dat))]
dat <- dat[is.na(t_confirm), t_confirm := hours(Inf)]
dat <- dat[get(index_var(dat)) <= t_confirm]
# carry-backward the sepsis-3 label for L = 24 hours
dat <- slide(dat, sep3_lab := max_or_na(sep3), before = hours(0L),
after = hours(24L))
# carry-forward the sepsis-3 label until t_confirm
dat <- dat[is.na(sep3_lab), sep3_lab := 0]
dat <- dat[, sep3_lab := cummax(sep3_lab), by = c(id_vars(dat))]
# remove extra columns & times before ICU
dat <- dat[, c("sep3", "t_confirm") := NULL]
dat <- dat[get(index_var(dat)) >= hours(0L)]The .parquet files generated by the above code can be used for training and testing.
Evaluation Code
After developing the AI model for prediction, a key step is to evaluate its potential clinical utility. For this purpose, we suggest an evaluation scheme, which can be performed using the patient_eval() function exposed in our repository. The data that needs to be fed into the function should be formatted as follows:
In particular, the input to the patient evaluation is a long-format table that contains a column named sep3_prob with the probability predictions. The label column sep3_lab determines whether it is desired to raise an alarm at this time point. The patient_eval() function then computes the sensitivity, specificity and the positive predictive value (PPV) over a range of prediction thresholds, and can be simply ran using the following code:
patient_eval(evl_dat, delta = hours(Inf), score_col = "sep3_prob",
tpp = "sep3_lab")Epidemiology
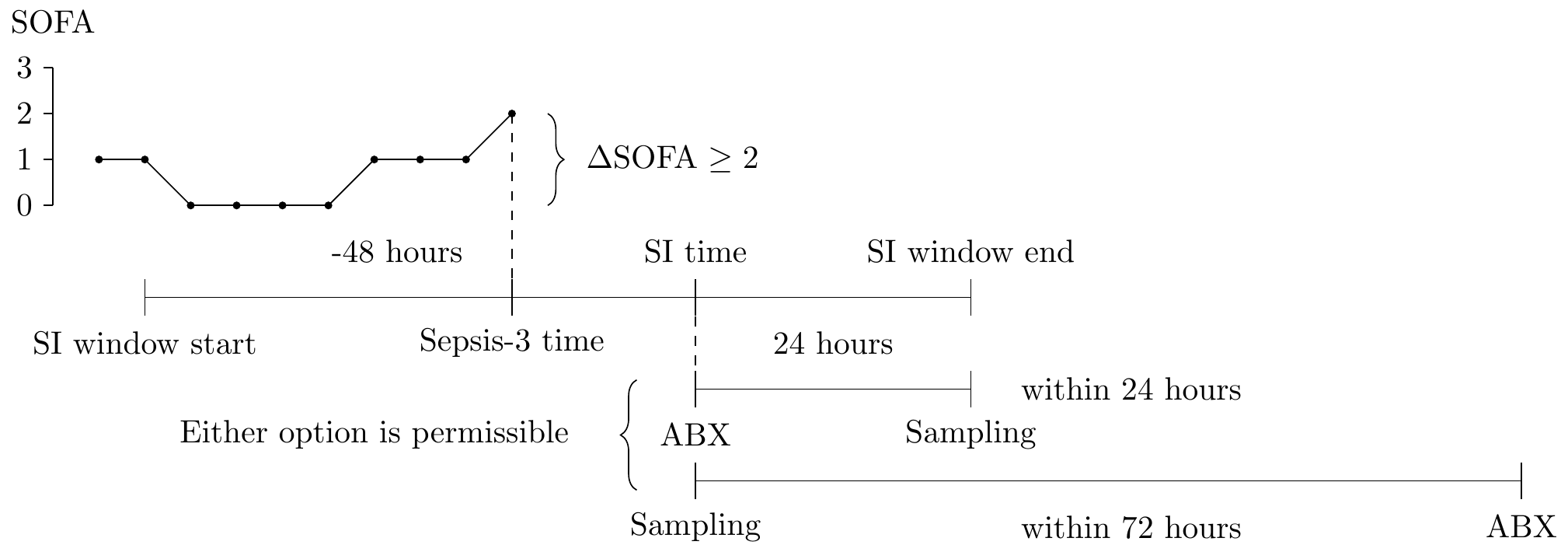
When consider prediction, the epidemiology of the prediction problem is often very relevant. For this reason, we investigate the following
- prevalence of sepsis-3 in each dataset,
- onset times of sepsis-3 in each dataset (\(t_{sep3}\)),
- time duration between sepsis-3 onset, and the time at which sepsis-3 is confirmed (\(t_{confirm} - t_{sep3}\)).